回合制游戏并行化初探

这个念头在我脑中成型已经有些年头了，我本人是回合制游戏《英雄无敌 3》的忠实粉丝，但是一盘游戏通常需要消耗三个小时以上的时间，PvP 则代价更高（因为普通选手无法像机器一样作出快速反应），为了避免高昂的等待时间，对战平台会限制每个选手每回合的时间。其余的回合制游戏（例如文明，俗称天亮）均存在类似的通病，在现代的社会节奏下均有式微的风险。

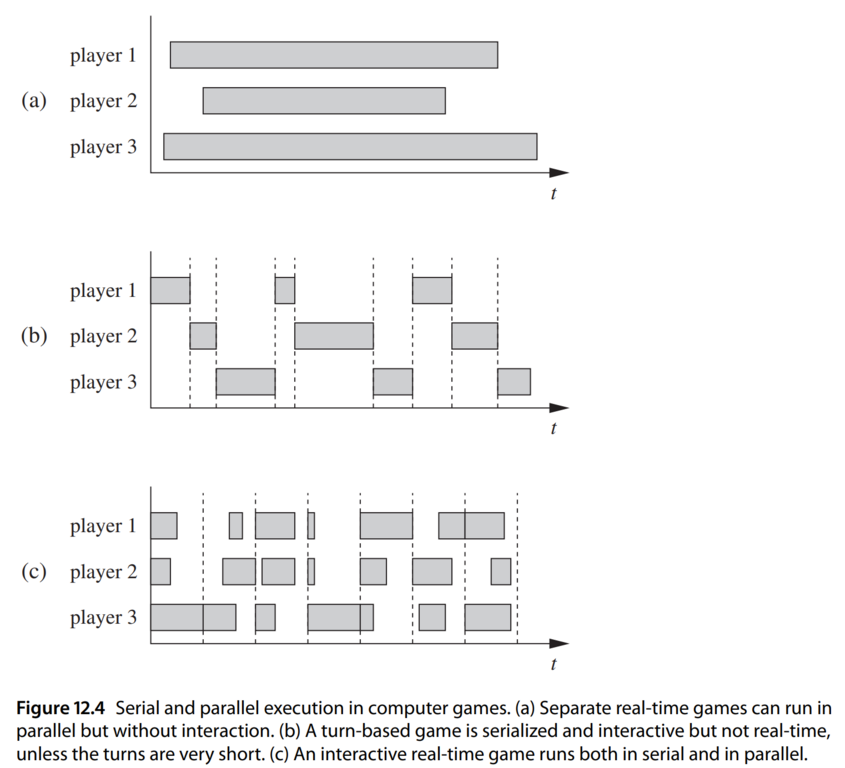
归根结底，回合制游戏为了解决不同用户操作之间的数据依赖问题，将所有玩家所有操作全部序列化（避免 race condition），执行流程如下图所示 ¹。

图中可见每个玩家都有很长的一段空窗时间，类比于 CPU 中的运算单元闲置。 而图(a) (即时游戏) 所有玩家都是饱和状态，因为服务器每个周期（xxx ms，人的肢体反应时间在 100ms 以上，因此我猜测周期不会比这个更短，否则对服务器的压力也会很大）会同步所有玩家的状态，避免了数据依赖的问题。

即时游戏的问题在与，所有玩家的时钟始终与服务器保持同步，而回合制游戏每个玩家可以控制自己的时钟 ²。玩家之间有 APM (action per minute) 上的巨大差异，即时游戏中手速快的玩家通常可以取得很大优势，导致了玩家与回合制游戏玩家思维模式上有一定差异。

我的目标是设计一种介于回合制和即时制之间的游戏机制，使得

• 每个玩家可以控制自己的时钟，不必与物理时钟同步。
• 玩家 \(i\) 在时间 \(t\) 时刻的操作对所有玩家在 \(t'>t\) 时刻的状态造成影响。
• （部分）并行化所有玩家的操作，保证对于所有玩家 \(1\cdots P\), 以及他们的操作序列 \(\{a^i_{j}\}_{j\in \mathbb{N}, i \in [P]}\) ，对于任意的物理操作过程 ³，在任意给定的 \(T\) 时刻，他们所处的状态 \(s^i_{T} = \hat{s}^i_{T}\) 其中 \(\hat{s}^i_{T}\) 是一个 oracle 模拟所有玩家操作序列在 \(T\) 时刻时 \(i\) 玩家的状态。
  • 完全相同可能是一个过强的要求，可以适当放宽限定，假设状态可以用一个离散的值来表示，那么 \(P(\mathbb{E}(s^i_{T}) - \hat{s}^i_{T}) \leq \epsilon\) 是一个可以接受的方案；更一般地，我们可以对局面进行估值，得到一个估值函数 \(f:S\rightarrow\mathbb{R}\) , 保证 \(P(\mathbb{E}(f(s^i_{T})) - f(\hat{s}^i_{T})) \leq \epsilon\) 即可 ⁴。

我尚未在中文社区见到有对类似问题的讨论，但我认为它是一个有思考价值的问题，且与计算机科学中很多传统的概念相似，在此抛砖引玉。